

Ken Iverson at Harvard University
Thousands of programming languages were invented in the first 50 years of the age of computing. Many of them were similar, and many followed a traditional, evolutionary path from their predecessors.
But some revolutionary languages had a slant that differentiated them from their more general-purpose brethren. LISP was for list processing. SNOBOL was for string manipulation. SIMSCRIPT was for simulation. And APL was for mathematics, with an emphasis on array processing.
What eventually became APL was first invented by Harvard professor Kenneth E. Iverson in 1957 as a mathematical notation, not as a computer programming language. Although other matrix-oriented symbol systems existed, including the concise tensor notation invented by Einstein, they were oriented more towards mathematical analysis and less towards synthesis of algorithms. Iverson, who was a student of Howard Aiken’s, taught what became known as “Iverson Notation” to his Harvard students to explain algorithms.
Iverson was hired by IBM in 1960 to work with Adin Falkoff and others on his notation. In his now famous 1962 book “A Programming Language” 1, he says the notation is for the description of “procedures…called algorithms or programs”, and that it is a language because it “exhibits considerable syntactic structure”. But at that point it was just a notation for people to read, not a language for programming computers. The book gives many examples of its use both as a descriptive tool (such as for documenting the definition of computer instruction sets) and as a means for expressing general algorithms (such as for sorting and searching). Anticipating resistance to something so novel, he says in the preface, “It is the central thesis of this book that the descriptive and analytical power of an adequate programming language amply repays the considerable effort required for its mastery.” Perhaps he was warning that mastering the language wasn’t trivial. Perhaps he was also signaling that, in his view, other notational languages were less than “adequate”.
The team, of course, soon saw that the notation could be turned into a language for programming computers. That language, which was called APL starting in 1966, emphasized array manipulation and used unconventional symbols. It was like no other computer program language that had been invented.
APL became popular when IBM introduced “APL\360” for their System/360 mainframe computer. Unlike most other languages at the time, APL\360 was also a complete interactive programming environment. The programmer, sitting at an electromechanical typewriter linked to a timeshared computer, could type APL statements and get an immediate response. Programs could be defined, debugged, run, and saved on a computer that was simultaneously being used by dozens of other people.
Written entirely in 360 assembly language, this version of APL took control of the whole machine. It implemented a complete timesharing operating system in addition to a high-level language.
With the permission of IBM, the Computer History Museum is pleased to make available the source code to the 1969-1972 “XM6” version of APL for the System/360 for non-commercial use.
The text file contains 37,567 lines, which includes code, macros, and global definitions. The 90 individual files are separated by ‘./ ADD” commands. To access this material, you must agree to the terms of the license displayed here, which permits only non-commercial use and does not give you the right to license it to third parties by posting copies elsewhere on the web.
Jürgen Winkelmann at ETH Zürich has done an amazing job of turning this source code into a runnable system. For more information, see MVT for APL Version 2.00.
Iverson’s book “A Programming Language” 1 uses a graphical notation that would have been difficult to directly use as a programming language for computers. He considered it an extension of matrix algebra, and used common mathematical typographic conventions like subscripts, superscripts, and distinctions based on the weight or font of characters. Here, for example, is a program for sorting numbers:
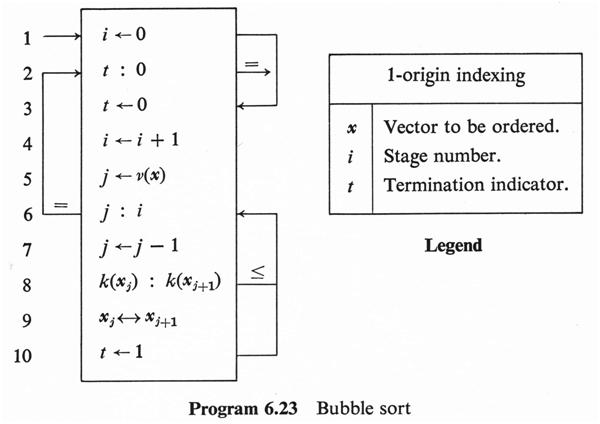
To linearize the notation for use as a computer programming language typed at a keyboard, the APL implementers certainly had to give up the use of labeled arrows for control transfers. But one feature that they were able to retain, to some extent, was the use of special symbols for primitive functions, as illustrated in this program that creates Huffman codes:

APL uses symbols that are closer to standard mathematics than programming. For example, the symbol for division is ÷, not /. To support the unconventional symbols, APL\360 used a custom-designed keyboard with special symbols in the upper case.

APL\360 used a custom-designed keyboard
Even so, there were more special characters than could fit on the keyboard, so some were typed by overstriking two characters. For example, the “grade up” character ⍋, a primitive operator used for sorting, was created by typing ∆ (shift H), then backspace, then ∣ (shift M). There was no room left for both upper- and lower-case letters, so APL supported only capital letters.
For printing programs, Iverson and Falkoff got IBM to design a special type ball for their 1050 and 2741 terminals, which used the IBM Selectric typewriter mechanism.


Now programs could be both typed in and printed. Here, for example, is the printed version a program from the APL Language manual 2 that computes the mathematical determinant of a matrix:

APL is a concise high-level programming language that differs from most others developed in the 1960s in several respects:
Order of evaluation: Expressions in APL are evaluated right-to-left, and there is no hierarchy of function precedence. For example, typing the expression
2×4+3
causes the computer to immediately type the resulting value
14
The value is not, as in many other languages that have operator precedence, 11. Of course, parentheses can be used to group a subexpression to change the evaluation order. The general rule is that the right argument of any function is the value of the expression to its right.
Automatic creation of vectors and arrays: A higher-dimensional structure is automatically created by evaluating an expression that returns it, and scalars can be freely mixed. For example,
A ← 2 + 1 2 3
creates the vector “1 2 3”, add the scalar 2 to it, and creates the variable A to hold the vector whose value is
3 4 5
Variables are never declared; they are created automatically and assume the size and shape of whatever expression is assigned to them.
A plethora of primitives: APL has a rich set of built-in functions (and “operators” that are applied to functions to yield different functions) that operate on scalar, vectors, arrays, even higher-dimensional objects, and combinations of them. For example, the expression to sum the numbers in the vector “A” created above is simply
+/A
where / is the “reduction” operator that causes the function to the left to be applied successively to all the elements of the operand to the right. The expression to compute the average of the numbers in A also uses the primitive function ρ to determine how many elements there are in A:
(+/A) ÷ ρA
Here are some tables from the 1970 “APL\360 User’s Manual” 3 that give a flavor of the power and sophistication of the built-in APL functions and operators.



APL encourages you to think differently about programming, and to use temporary high-dimensional data structures as intermediate values that are then reduced using the powerful primitives. A famous example is the following short but complete program to compute all the prime numbers up to R.
(~T∊T∘.×T)/T←1↓⍳R
Here is how this expression is evaluated:
|
subexpression |
meaning |
value if R is 6 |
|||||||||||||||||||||||||
|
⍳R |
Generate a vector of numbers from 1 to R. |
1 2 3 4 5 6 |
|||||||||||||||||||||||||
|
T←1↓ |
Drop the first element of the vector and assign the rest to the temporary vector T. |
2 3 4 5 6 |
|||||||||||||||||||||||||
|
T∘.×T |
Create the multiplication outer product: a table that holds the result of multiplying each element of T by each element of T. |
|
|||||||||||||||||||||||||
|
T∊ |
Use the “set membership” operator to find which elements of T are in the table. |
0 0 1 0 1 |
|||||||||||||||||||||||||
|
~ |
Negate the result to identify which elements of T are not in the table. These are the integers which do not have any multiples in the table. |
1 1 0 1 0 |
|||||||||||||||||||||||||
|
( )/T |
Select the elements of T which we have identified. These are all the primes less than R. |
2 3 5 |
Note that there are no loops in this program. The power of APL expressions means that conditional branches and loops are required far less often than in more traditional programming languages.
APL operators can be used in easy ways for all sorts of computations that would usually require loops. For example, an expression that computes the number of elements of the vector X that are greater than 100 is
+/X>100
It works because X>100 returns a bit vector of 0’s and 1’s showing which elements of X are greater than 100, and +/ adds up all the bits in that vector.
But conditional execution and loops are, of course, sometimes needed. In the light of later developments in structured programming, APL’s only primitive for control transfer, the “GO TO LINE x” statement →, is particularly weak. Here is an example of a function that computes the greatest common divisor of its two arguments. The last statement creates a loop by branching to the beginning. In line 2, conditional transfer of control to line 0 causes the function to exit and return the value last assigned to G.
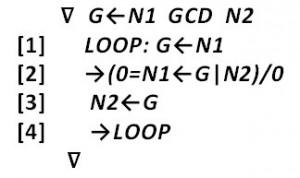
To learn more about the 1960’s APL language, see the “APL Language” reference manual 2 and Paul Berry’s 1969 “APL\360 Primer” 4.
The language has of course evolved over the years, and more recent versions include control structures such as IF-THEN-ELSE.
The first computer implementation of APL notation was a batch-oriented language interpreter written in FORTRAN in 1965 for the IBM 7090 mainframe computer, by Larry Breed at the IBM Research Center in Yorktown Heights NY and Philip Abrams, then a graduate student at Stanford University.
The first interactive version was written soon after for the 7093 (an experimental 7090 with virtual memory) by Larry Breed and Roger Moore. It ran under the TSM timesharing system and was whimsically called “IVSYS”, which rhymes with “IBSYS”, the name for the standard 7090 operating system. In a 2012 email Breed says,
Another implementation of a subset of the language was done in 1967 for the IBM 1130 minicomputer.
The first implementation of APL to get widespread use outside of IBM was for the IBM System/360. Called “APL\360”, it went into service first within IBM in November 1966. (The notation “APL\360″, since the backslash was the APL “expansion” operator, also had a hidden meaning: “APL expands the 360″).
Breed says of the time just before,
By August 1968 APL\360 was available to IBM customers as an unsupported (“Type III”) program in IBM’s “Contributed Program Library” 5. The principal implementers were Larry Breed, Dick Lathwell, and Roger Moore; others who had contributed were Adin Falkoff and Luther Woodrum.

Early APL developers, from left to right: Dick Lathwell, Ken Iverson, Roger Moore, Adin Falkoff, Phil Abrams, Larry Breed. The photo was taken about 1983.
Because of the dynamic nature of APL variables, APL\360 was implemented as an interpreter, not as a compiler that generated machine code. Programs were stored in an internal form called a “codestring” that directly corresponded to what the user had typed. The interpreter would then examine the codestring as the program executed, and dynamically allocate and reconfigure variables as expressions were evaluated.
The first versions of APL\360 took control of the entire machine. It was thus a combination operating system, file system, timesharing monitor, command interpreter, and programming language. Given the limited main memory, user workspaces were swapped out to drum or disk as needed. Performance was impressive, which Larry Breed attributes, in his clear and succinct description of the implementation 6, to the ability to tailor the operating system to the requirements of the language.
APL\360 was a conversational language that provided fast response and efficient execution for as many as 50 simultaneous users. Each user had an “active workspace” that held programs, variables, and the state of suspended program execution. System commands like “)LOAD”, “)SAVE”, and “)COPY” maintained the user’s library of stored workspaces. Other system commands controlled language features; for example, with “)ORIGIN” the programmer could control whether vectors and arrays are numbered starting with 0 or 1.
APL was the first introduction to interactive timesharing for many in the generation of programmers who had suffered through batch programming with punched cards.
Even before it was a computer programming language, Iverson Notation was useful as a language for documenting algorithms for people. The classic example is the formal definition of the instruction-set architecture of the new IBM System/360 computer, which was published in an article in the IBM Systems Journal by Adin Falkoff, Ken Iverson, and Ed Sussenguth in 1965 7.
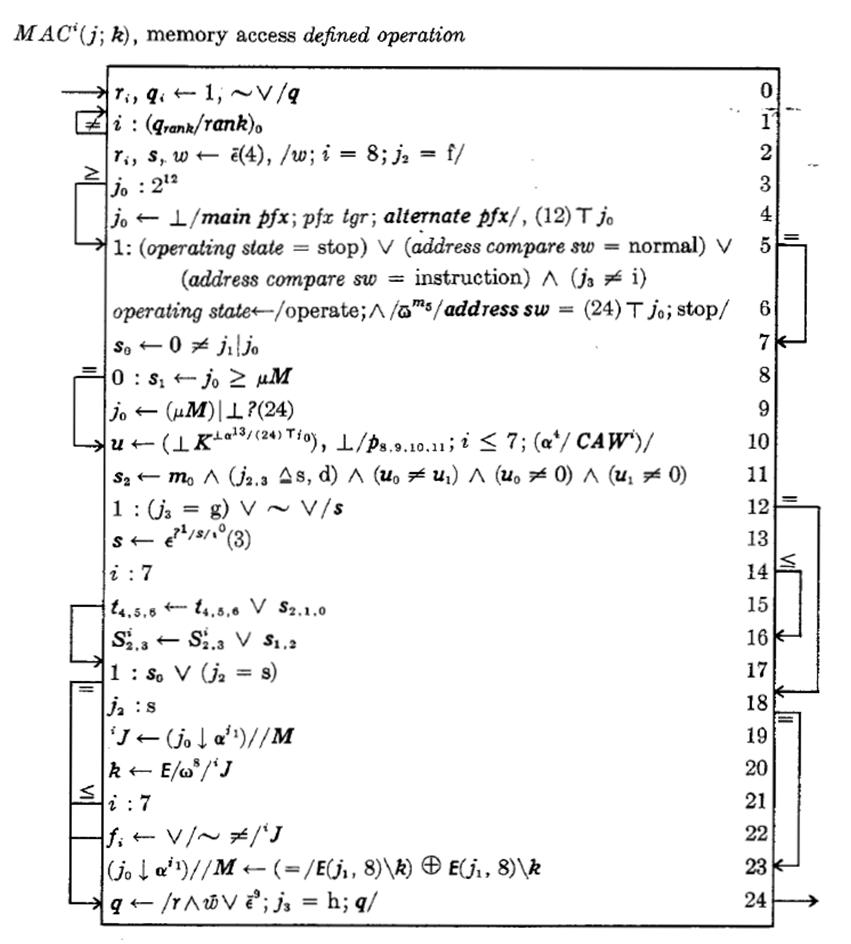 But the text provided in the paper is much more than that. It is a line-by-line explanation of the formal description, which means that it is also a demonstration and explanation of APL’s descriptive power.
But the text provided in the paper is much more than that. It is a line-by-line explanation of the formal description, which means that it is also a demonstration and explanation of APL’s descriptive power.
The notation used the graphical style for control transfers that was in Iverson’s book. Here, for example, is the description of a memory access operation.
It was the transition of APL from a notation for publication into an interactive computer programming language that made it flourish. When the APL\360 implementation was available, IBM and others stimulated use by producing diverse applications such as these:
Many of these applications emphasized interactivity, which provided a huge productivity increase compared to the batch-job processing more typical at the time. In addition, APL allowed applications to be developed much more quickly. In a 2012 email, Larry Breed noted,
The areas in which APL had the greatest penetration were in scientific, actuarial, statistical, and financial applications. For details about the progression of APL in its first 25 years, see the special 1991 issue of the IBM System Journal 10 with 12 papers and one essay on the subject.
APL was not originally designed as a programming language. As Iverson said,
With so many terse and unusual symbols, APL computer programs, like the mathematical notation that inspired it, has a conciseness and elegance many find appealing. APL attracts fanatic adherents. Alan Perlis (the first recipient of the ACM’s Turing Award, in 1966) was one:
Many find the freedom of expression in APL liberating.
But APL programs are often cryptic and hard to decode. Some have joked that it is a “write-only language” because even the author of a program might have trouble understanding it later. It inspires programming trickery. The challenge of writing an APL “one-liner” to implement a complete complex algorithm is hard to resist. Here, for example, are two different APL one-liners that implement versions of John Conway’s “Game of Life“:
life←{↑1 ω∨.∧3 4=+/,¯1 0 1∘.⊖¯1 0 1∘.⌽⊂ω}
![]()
Not for the faint-hearted, clearly. Dutch computer scientist Edsger Dijkstra said,
But fans of APL would say that cryptic APL coding is a bad programming style that can be an affliction with any language. APL provides a richer palette for expressing algorithms, the argument goes, so you can solve harder problems faster and with less irrelevant syntactic clutter.
Whatever your view, APL and the languages it inspired, such as APL2 and J, are still an active part of the diverse programming language universe.

Kenneth Eugene Iverson was born on December 17, 1920 on a farm near Camrose, Alberta, Canada. He was educated in rural one-room schools until the end of 9th grade, when he dropped out of school because it was the height of the Depression and there was work to do on the family farm. He later said the only purpose of continuing his schooling would have been to become a schoolteacher, and that was a profession he decidedly did not want. During the long winter months he studied calculus on his own.

He was drafted in 1942, and during his service he took enough correspondence courses to almost complete high school. After the military service he earned a B.A. in both mathematics and physics from Queen’s University in Kingston Ontario, and then an M.A. in physics from Harvard University. In 1954 he completed a PhD under computer pioneer Howard Aiken, with a thesis titled “Machine Solutions of Linear Differential Equations: Applications to a Dynamic Economic Model”.
After completing his doctorate, Iverson joined the Harvard faculty to teach in Aiken’s new automatic data processing program. He was there for one year as an Instructor, and for five years as an Assistant Professor. He became increasingly frustrated with the inadequacy of conventional mathematical notation for expressing algorithms, so he began to invent his own.
In 1960 Iverson joined the new IBM Research Center in Yorktown Heights, New York, on the advice of Frederick Brooks, who had been one of his teaching fellows at Harvard and was now at IBM. The two collaborated on the continuing development of the new notation. In 1962 Ken published the now-classic book “A Programming Language” 1, the title of which gave the name APL to the notation which had up until then been informally called “Iverson’s notation”.
Iverson continued to work on the development of APL throughout his tenure at IBM. In 1980 he left IBM and returned to Canada to work for I.P. Sharp Associates, which had established an APL-based timesharing service.

In 1987 he “retired from paid employment” and turned his full attention to the development of a more modern dialect of APL. APL was successfully being used for commercial purposes, but Iverson wanted to develop a new simple executable notation more suitable for teaching, which would be available at low cost. The first implementation of this language, called J, was announced at the APL90 Users’ Conference.
Iverson’s ability to create such languages came from his “sheer enjoyment of language and words,” recalls his daughter Janet Cramer. “He read dictionaries like people read novels.” Iverson thought it was important that language, both English and mathematics, communicate clearly and concisely.
With collaborators that included his son Eric, Iverson continued to work on the development of J, and he continued to publish prolifically. On Saturday, October 16, 2004 he suffered a stroke –while working on a J tutorial — and died three days later on October 19, at the age of 83.
There are many stories about Ken Iverson. Here are a few: